Dynamical Mean Field Studies of Infinite Layer Nickelates: Physics Results and Methodological Implications

1 Introduction

The identification of a new class of superconductors is a momentous event. Ways in which the new superconductors are similar to or different from previously known materials can drive new insights into the microscopic origin of this fundamentally mysterious quantum many-body phenomenon. The discovery [1, 2] of superconductivity in layered copper-oxide materials sparked a revolution in condensed matter physics and materials science, because the transition temperatures were very high relative to other materials known at the time. Additionally, many aspects both of the superconductivity and of the non-superconducting (“normal state”) physics differed sharply from the predictions of conventional theory [3] in ways that made it obvious that interacting electron physics beyond mean field theory could have consequences of fundamental physics interest that approach (and in a few niche cases reach) commercial viability.

The very recent discovery [4] of superconductivity in the layered d⁹ nickelates was also momentous because the superconductivity was theoretically anticipated [5] on the basis of a chemical and structural similarity to the cuprates. Understanding the properties of the superconducting nickelates provides an immense scientific opportunity to sharpen our understanding of the relation between crystal structure and local chemistry on the one hand and important phenomena such as superconductivity on the other.

The relationship between physical phenomena and crystal structure/local chemistry is the central question in the theory of quantum materials. The theory of quantum materials is one instance of the quantum many-body problem, one of the grand scientific challenges of our time. The quantum many-body problem is in essence a problem of data compression: as is well known, many-particle quantum mechanics is formulated in a Hilbert space of a size that grows exponentially with the number of degrees of freedom while quantum entanglement in general and Fermi statistics in particular implies that delicate phase relationships between different states are of crucial importance. Incorporating the chemical realism needed to understand and predict material properties requires acting on this Hilbert space with a Hamiltonian matrix that involves a number of parameters which grows as a very high power of the number of degrees of freedom. All solutions of the quantum many-body problem require both reducing the number of degrees of freedom and the number of interaction parameters to a manageable level (“downfolding” the physics to a simpler systems, typically a “low energy theory”) and then handling the “model system” analysis of the still exponentially large and severely entangled Hilbert space of the downfolded theory.

Three decades of intense work have led to a rough consensus, generally although not universally accepted, that the low energy theory for the copper-oxide materials is some variant of the two dimensional one band Hubbard model. The relation of the model parameters to the precise chemistry and structure is reasonably well understood, and the properties of the simplest instantiations of this model are starting to come into focus [6–8]. The recent discovery of superconductivity in layered d⁹ nickelates such as NdNiO₂ takes these questions to a new level. While many aspects of the crystal structure and chemistry are similar to those of the cuprates, in the nickelate family of materials multiple bands cross the Fermi surface and more interactions may be relevant. A crucial question is whether these effects are minor, so that the important physics of the nickelates is similar to that of the cuprates, or whether the low energy physics is richer and more complex in nickelates than in cuprates.

Various interacting models have been proposed for NdNiO₂. The simplest interacting lattice model is a single Ni $d_{x^2-y^2}$ orbital Hubbard model with an additional electron reservoir to mimic the self-doping effect from other bands that exist near the Fermi level. Kitatani et al. used this interacting model to directly estimate the superconducting transition temperatures [9]. Hepting et al. [10] and Been et al. [11] used a two-orbital model including Ni-$d_{x^2-y^2}$ orbital and a lanthanide element $d_{3z^2-r^2}$-like orbital with an interaction only on the Ni-$d_{x^2-y^2}$ orbital. A number of studies [12–17] focus on a different type of two-orbital models that consists of two Ni-d orbitals. Hu et al. [12] include Ni-$d_{x^2-y^2}$ and Ni-d_xy orbitals, while Zhang et al. [14], Werner et al. [13], and Kang et al. [15] and Wan et al. [17] include Ni-$d_{x^2-y^2}$ and Ni-$d_{3z^2-r^2}$ orbitals. These two-orbital models not only includes the local interaction on each Ni d orbital, but also takes into account the Hund’s coupling between the two Ni d orbitals, relevant if the Ni high-spin S = 1 d⁸ state is relevant. Wu et al. [18] include Ni-$d_{x^2-y^2}$ orbital, neodymium $d_{3z^2-r^2}$ orbital, and neodymium d_xy orbital. Local interactions are added on both Ni-$d_{x^2-y^2}$ orbital and neodymium d orbitals. This model is used to calculate the spin susceptibility and to estimate the superconducting transition temperature in the weak-coupling limit. Nomura et al. [19] compare two different three-orbital basis: one is identical to that of Ref. [18] and the other one is Ni $d_{x^2-y^2}$ orbital, lanthanide $d_{3z^2-r^2}$ orbital and interstitial s orbital. Strength of local interactions on all three orbitals is estimated. The model is used to study the screening effects on the Hubbard U of Ni-$d_{x^2-y^2}$ orbital. A different flavor of three-orbital model is employed by Lechermann [20], which consists of Ni $d_{x^2-y^2}$ and Ni $d_{3z^2-r^2}$ orbitals as well as a self-doping orbital. The model emphasizes the importance of multi-orbital processes in RNiO₂. Gu et al. [21] use a four-orbital model: Ni d_xy orbital, lanthanide $d_{3z^2-r^2}$ orbital, lanthanide d_xy orbital and interstitial s orbital. Local interaction is added on Ni-$d_{x^2-y^2}$. The model is used to study the interplay between hybridization and correlation effects and to calculate the phase diagram. Gao et al. [22] construct a general four-orbital model B_1g@1a⊕A_1g@1b which consists of two Ni-d orbitals and two lanthanide d orbitals. The model is used to study the topological property of the Fermi surface. All the above models focus on Ni-d and/or lanthanide d orbitals. A number of studies also explicitly take into account oxygen p states with local interactions added on Ni-d orbitals [20, 23–25]. Jiang et al. [23] study a hole doped system that consists of a Ni d⁹ impurity properly embedded in an infinite square lattice of O p⁶ ions. This impurity model is used to argue that in the NiO₂ layer, the strong pd hybridization may favor a S = 0 hole-doped state with ¹A1 symmetry, similar to superconducting cuprates.

Which of the plethora of theoretical models is most relevant is an important question. This review will present a perspective on what has been learned from the density functional theory (DFT) plus dynamical mean field theory (DMFT) about the many body electronic structure and the relevant low energy model and also what has been learned about the methods in the context of applying them to the layered nickelates.

2 Overview

2.1 Crystal Structure and Basic Chemistry

The copper oxide and layered d⁹ nickelate materials are transition metal oxide (TMO) compounds that share the common structural motif of the CuO₂/NiO₂ plane. We focus first on the conceptually simplest materials, “infinite layer” CaCuO₂ and NdNiO₂ [panel (A) of Figure 1] in which the transition metal ions occupy the vertices of a square planar array with the oxygen ions at the midpoints of the edges. In their bulk, three dimensional form these materials are stacks of transition metal/oxygen planes, with the Ca/Nd ions located half-way between planes, above the centers of the squares formed by four transition metal ions.

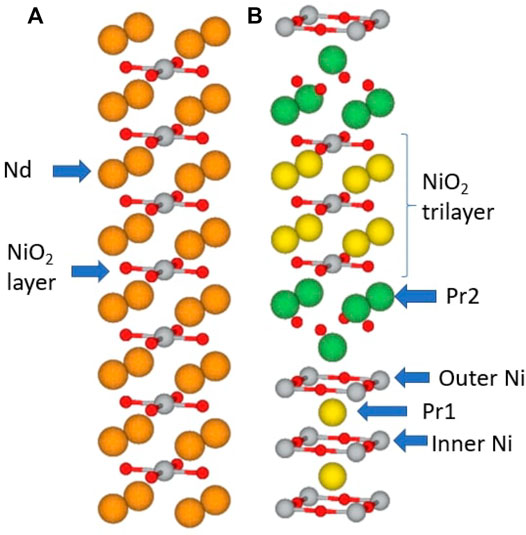
FIGURE 1. (A): crystal structure of infinite layer NdNiO₂ in the P4/mmm structure. (B): crystal structure of trilayer Pr₄Ni₃O₈ in the I4/mmm structure. Ni atoms are shown in silver, O in red, Nd in orange, Pr1 in yellow, and Pr2 in green. From Ref. [25] and the crystal structures are visualized using Vesta [115].

The CuO₂/NiO₂ plane motif may be combined in many ways, yielding a wide variety of compounds with somewhat similar properties but with many differences of detail. The very large number of cuprate materials will not be discussed here. In the nickelate materials, the infinite layer compounds can in principle be realized with all rare-earth elements R as A-site cation [26]. So far R = La, Pr, and Nd have been synthesized. In addition, multilayer variants R_1+mNi_mO_2m+2 are known, consisting of groups of m NdNiO₂ planes separated by effectively insulating spacer layers of Nd and O. To date, m = 3, 4, 5 have been synthesized. The m = 3 material is shown in panel (B) of Figure 1; the plane labelled Pr2 is the spacer layer. Some charge transfer (CT) to the spacer layers occurs, leading to a doping of the NiO₂ planes that is different than that of the infinite layer compounds, but apart from this the basic electronic physics of the layered compounds is believed to be very similar to that of the infinite layer compounds [27]. In this article we consider the compounds as interchangeable.

Qualitative chemical (“formal valence”) considerations suggest that the electronic configurations of the ions are Ca²⁺${\mathrm{C}\mathrm{u}}^{2+}{\left[{\mathrm{O}}^{2-}\right]}_2$ and Nd³⁺${\mathrm{N}\mathrm{i}}^{1+}{\left[{\mathrm{O}}^{2-}\right]}_2$ corresponding in both cases to a transition metal d⁹ configuration (one hole in the d-shell), and standard considerations of ligand field theory indicate that the hole resides in the transition metal $d_{x^2-y^2}$ orbital. Varying the chemical formula (e.g., by replacing a fraction x of the Nd³⁺ with Sr²⁺ can lead to changes in the Cu/Ni formal valence to d^9±x (electron or hole doping) and in both material families electron and hole doping leads to dramatic changes in physical properties; in particular, superconductivity occurs only in relatively narrow electron or hole doping ranges not including the nominal d⁹ valence.

Formal valence considerations are only a rough approximation to the actual electronic states because in a solid the charge on an ion is not conserved. Quantitatively or qualitatively important roles may be played by charge transfer processes including fluctuations that move an electron from an O to a transition metal (producing a $d^{10}\underline{L}$ configuration, where $\underline{L}$ refers to a hole in the oxygen ligand) or from the transition metal to the rare earth/alkali producing e.g., an Ni d⁸ Nd ²⁺ configuration or between two transition metal ions, producing a d⁸ − d¹⁰ pair. Especially for Ni based transition metal oxides (TMO) it is well known that Ni-O bonds are highly covalent and hybridization effects lead to drastic deviations from the formal atomic orbital occupation picture [28, 29]. The low energy theory of the copper-oxide materials is generally although not universally, accepted to involve one band, of mixed Cu-$d_{x^2-y^2}$ and O(2p) character and with an essentially two dimensional dispersion and with relatively strong, relatively local interactions derived from intra-d Coulomb matrix elements but substantially affected in magnitude by CT and screening processes involving the O ions (the rare earth/alkali ions such as the Ca in CaCuO₂ are believed to be electronically inert on these scales) [3]. Important to this finding is the observation that the relevant configurations of the Cu(3d) states are d⁹ and d¹⁰; this simple multiplet structure strongly constrains the possible interaction terms. The low energy theory is thus a variant of the two dimensional Hubbard model, possibly including longer ranged interactions.

In the layered d⁹ nickelates such as NdNiO₂ the situation is richer. Multiple bands cross the Fermi surface, while the potential relevance of d⁸ configurations raises the possibility that multiplet (“Hund’s”) interactions governing the relative energetics of different configurations of TMO d-electrons are relevant to the low energy physics. A fundamental question is whether this additional physics plays an important role in the low energy correlation physics such as superconductivity or whether the correlation physics of the nickelates is in essence similar to that of the cuprates.

2.2 Downfolding and the DFT + DMFT Methodology

In the context of quantum materials the process of defining an appropriately reduced model from a high energy, more chemically realistic, “all orbital” description is referred to as “downfolding”. Downfolding starts from the use of a mean field like approximation such as density functional theory to define a single-particle basis (e.g., the Kohn-Sham eigenstates within a broad energy region) that is for all practical purposes complete. Then a subspace of this set of states is selected and the Hamiltonian is appropriately projected onto the subspace. The required projection is more sophisticated than simply taking the matrix elements of the Hamiltonian between states in the subspace: screening of the retained interactions by processes involving states that are not retained must be incorporated and correlation induced shifts in relative energy splittings of different states (“double counting corrections”) must be managed correctly. Further, since the purpose is to obtain something that can be solved (perhaps approximately), the specifics of downfolding are intertwined with the method of solution of the resulting theory.

While one important goal of a downfolding process is to obtain a truly low energy theory (defined, say on the ±0.5 eV interval around the chemical potential that is relevant for analysis of transport and of low energy instabilities such as superconductivity), in the case of transition metal oxides an intermediate step of downfolding to a reduced model defined in a wider energy range but with truncated interactions has been found to be very useful. This intermediate step is motivated by the physical/chemical intuition that in transition metal oxides the most relevant interactions are the site local charging (“U”) and multiplet (“J”) interactions that control the energy levels of a partly filled d shell on a transition metal ion and by the success of the DMFT approximation in treating the resulting physics.

The DFT + DMFT methodology is a specific downfolding method based on the idea that both the important interactions and the correlation physics they induce are spatially local in a sense defined more precisely below. It is closely related to the DFT + U method inmpmllemented in standard DFT codes; indeed the DFT + U method is in effect the hartreee approximation to the DFT + DMFT method. The locality of the interactions greatly reduces the number of relevant interaction parameters (i.e., the complexity of the interacting Hamiltonian that must be solved) while the locality of the correlation physics drastically reduces the severity of entanglement effects, enabling a tractable solution of the resulting correlation problem. The method is now a work-horse of correlated electron materials science and the nickelate materials provide an interesting test of both the assumptions that go into the methodology and the results it produces.

The DFT + DMFT methodology [30, 31] uses a DFT calculation to define a set of correlated orbitals (for example the Ni d-orbitals), the hybridization of these orbitals to each other and to other orbitals, presumed to be uncorrelated, and also involves a prescription for associating site local interactions to the correlated orbitals. The resulting downfolded system may be thought of a kind of generalized multi-orbital Hubbard model involving correlated sites coupled to uncorrelated ones and is solved in the DMFT (locality of correlation physics) approximation which reduces the problem to the solution of a quantum impurity model (set of local orbitals coupled to a non-interacting bath) plus a self-consistency condition. Finally, in a charge self-consistent (CSC) step which is sometimes omitted, the full charge density of the system is obtained and fed back in to the density functional theory; the correlated orbitals are redefined, and the process is repeated until complete self consistency is obtained. This process is visualized in Figure 2. Importantly, the CSC DFT + DMFT equations can be derived as the stationarity conditions of a general functional describing the electronic structure ab-initio [31] within the DMFT approximations.

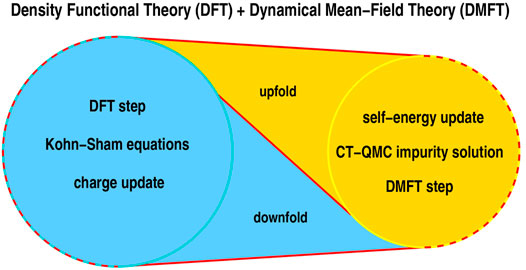
FIGURE 2. Principle DFT + DMFT method as hybrid scheme, working as a ratchet with up- and downfolding links. One starts from a converged KS-DFT calculation and downfolds to the correlated subspace where a DMFT step is performed. This asks mainly for the solution of a quantum-impurity problem [here conducted via continuous-time quantum-Monte Carlo (CT-QMC)], yielding a local self-energy. That self-energy is upfolded to the Bloch space of the DFT problem and used to revise the electronic charge density. Using the latter, a new KS potential is generated and a novel DFT step performed, which is followed by the next downfolding, etc. This cycle is performed until self-consistency in the charge density and the self-energy is achieved. Adapted from Ref. [116].

In first instance, DMFT delivers results for the electron (one-particle) Green’s function $\widehat{G}$, which is directly connected to the physical spectral function:

From solving the impurity problem within DMFT the atomic multiplet nature of the correlated manifold can also be analyzed from the many-body density matrix. The computed spectral functions can be compared directly to photoemission measurements [32, 33] and considerable intuition about the physics can be gained from the many body density matrices. Furthermore, symmetry broken phases such as superconductivity and magnetic phase can be addressed, and transport coefficients can be estimated. Momentum dependent susceptibilities and vertex functions can also be constructed, albeit with much more computational effort.

The important technical steps in implementing the dynamical mean field approximation are the construction of the correlated orbitals and their coupling to the uncorrelated orbitals and the computation of the interactions among electrons in these orbitals.

3 Methods

The DFT + DMFT methodology is formulated in terms of the single particle Green function, defined on the Matsubara (imaginary frequency) axis for a periodic solid as

Here k is a wavevector in the first Brillouin zone of the solid, μ is the chemical potential, H_ref is a reference single-particle (non-interacting) Hamiltonian and the self energy operator $\widehat{\mathrm{\Sigma }}$ parametrizes the difference between physical electron propagation and the predictions of the reference single-particle Hamiltonian. If the theory is solved exactly, the choice of reference Hamiltonian is immaterial: it just provides a starting point for calculations. However, actual calculations involve approximations and require the use of a computational basis that is a subset of the full set of all single-particle eigenstates of H_ref; in this circumstance, the choice of H_ref and the choice of basis functions will influence the final result.

Here, we take H_ref to be the Kohn-Sham Hamiltonian produced by a specified density functional theory combined with a “double counting (DC) correction” and ${\widehat{\mathrm{\Sigma }}}_{\mathbf{k}}^{\nu ,{\nu }^{\prime }}$ is a matrix in the space spanned by the eigenstates ψ_νk(r) of H_ref, which is constructed using a locality ansatz described more explicitly below. The different “pure” DFT exchange-correlation functionals give very similar results and will not be discussed explicitly here. However, extensions of DFT such as self interaction correction (SIC) DFT [34] do lead to different results, as discussed below. For further reading we refer to review articles, i.e., Ref. [35].

In embedding theories such as DFT + DMFT one defines on physical grounds a subset of correlated orbitals (in the cuprate/nickelate context the transition metal d-orbitals) and retains only the site-local matrix elements of the self energy among these orbitals and the site-local interactions that contribute to these matrix elements. These site-local self energy matrix elements are then calculated via a mapping to a quantum impurity model with the local Hamiltonian (crystal field levels plus interactions) of the full model and a self-consistently determined coupling to a bath in the form of a so called “hybridization function”; the result is self-consistently embedded into the full electronic structure.

The key conceptual issues in the method are the construction of the local orbitals and the specification of the interactions between them. These issues are discussed in the next two subsections.

3.1 Quantum Embedding: Construction of the Localized Orbitals

The first step in this procedure is to precisely define a set of orbitals ${\varphi }_m^{R_i}$ centered on sites R_i. These orbitals define a basis in which the self energy and local interactions are computed. Within the DFT + DMFT community many approaches to define these local orbitals have been introduced. All methods explicitly or implicitly use a set of so called “projector functions”:

which specify the relation of the local orbitals ${\varphi }_m^{R_i}$ to the Kohn-Sham (KS) eigenstates ψ_ν,k. The P operators are termed projectors because in the general case there are fewer localized orbitals m than there are Kohn-Sham eigenstates ν.

The projector functions allow one to “upfold” a self energy calculated in the orbital (R_i, m) basis to the Kohn-Sham basis as

Here we have written Eq. 4 for the DMFT ansatz of a self energy that is site local in the orbital basis. In general the self-energy can also contain multiple sites embedded as a cluster impurity. However, in this case one has to carefully consider breaking of symmetries due to the geometry of the lattice.

The full Green function Eq. 2, a matrix in the set of Kohn-Sham bands, is then written as

The ‘downfolded’ site-local lattice Green function $G_{\text{QI};R_i}^{m{m}^{\prime }}$ in the orbital basis is given as

which allows to construct the dynamic Weiss field of the quantum impurity problem in DMFT via a Dyson equation:

${\mathcal{G}}_{m{m}^{\prime }}^0$ connects the impurity and the bath, from which a hybridization function for the Anderson impurity model (AIM) can be constructed.

Solving the impurity problem gives a new self-energy (Eq. 4), defining a new lattice Green function, and hence a new local Green function. This procedure is performed until convergence is reached and ${\mathcal{G}}^0$ does not change further.

The DMFT converged lattice Green function Eq. 5 can be used to construct a new charge density:

which serves as input for DFT in a CSC DFT + DMFT calculation. From this a new charge density from DMFT a new set of Kohn-Sham (KS) orbitals, projectors and interactions are defined and the DMFT equations are solved again. This procedure is repeated until the charge density converges. The effect of this additional charge self consistency loop is sometimes small, but in many cases can have important quantitative influence in the results [36], and is technically needed to evaluate energies within the DFT + DMFT formalism [31].

3.1.1 Projected Atomic Orbitals

One choice for constructing the projector functions is the projected atomic orbitals (PLO) methodology [37–39], in which one introduces a set of atomic-like correlated orbitals $|{\tilde{\varphi }}_m^R\rangle$, which are centered on the positions R of the ions of interest, have the symmetry appropriate to the correlated orbital of interest (e.g. transition metal d), and are set to zero for distances $|\vec{r}-\vec{R}|$ around R greater than some preset value. In this formalism a first set of projectors is then defined from Eq. 3 as

The downfolded orbitals describing the correlated subspace are computed as

here, $\mathcal{W}(\mathbf{k})$ notates the fact that all practical calculations retain only a subset of KS states within a possibly k-dependent window $\mathcal{W}(\mathbf{k})$. Since the sum over ν is not complete, as it runs only over $\mathcal{W}(\mathbf{k})$, the $|{\bar{\varphi }}_m^{R_i}\rangle$ must be orthonormalized. The result after orthonormalization are functions $|{\varphi }_m^{R_i}\rangle$ that deviate to some degree from the originally defined atomic like states like states $|{\tilde{\varphi }}_m^{R_i}\rangle$, and in particular have tails that extend outside the originally defined radius. These functions may be viewed as Wannier functions as defined as in Eq. 11, with the procedure described above corresponding to a prescription for constructing some elements of the U matrices. These new states are then used in Eq. 3 to construct the projectors $P_{\nu ,\mathbf{k}}^{R_i,m}$, which are actually used in the formalism.

The window $\mathcal{W}(\mathbf{k})$ effectively controls how localized the resulting states are, and one strategy is to formulate the problem in as wide a range as feasible, to make the $|{\varphi }_m^{R_i}\rangle$ very localized. However, a narrower energy window has the advantages of focusing attention on states that are more directly related to the low energy physics of interest and of providing a theory with lower intrinsic energy scales.

3.1.2 Maximally Localized Wannier Functions for Downfolding

One may also obtain the projector functions via the Wannier construction introduced by Marzari and Vanderbilt [40], in which one defines N spatially localized Wannier functions (WFs) as Fourier transforms of linear combinations of N KS states via

Here the $U_{\nu \alpha }^{*(\mathbf{k})}$ are the components of a family of unitary transformations (one at each k) and are chosen to optimize specific properties of the $|w_{\alpha }^{R_i}\rangle$. The most common choice, referred to as the maximally localized Wannier function (MLWF) method, is to choose the $U_{\nu \alpha }^{*(\mathbf{k})}$ to minimize the mean square spread of all WFs in the unit cell [40]. Alternatively, one can construct selectively localized Wannier functions (SLWFs) by performing the spread minimization only for certain WFs [41].

A subset of the Wannier functions, labelled by m, are identified with the correlated orbitals and the Wannier construction in Eq. 11 implies that projectors can be identified as

This construction is implemented in the software package Wannier90 (W90) [42].

The initial seed for $U_{\mu \alpha }^{(k)}$ are typically obtained by projections on atomic orbitals similar to the PLOs above. These are orthonormalized, and then the orthonormalized functions are used as a starting point for the spread minimization. The additional optimization process leads to differences between the MLWF and PLO procedures.

The number of Kohn-Sham bands N_B used in the Wannierization process can be chosen similar to the projector method above via a window $\mathcal{W}(\mathbf{k})$ which is ideally set to contain a group of bands separated by energy gaps from all other bands in the solid. If N_B is larger than the number of desired Wannier orbitals then a disentanglement procedure is performed, producing a set of N optimized Bloch states $|{\mathrm{\Psi }}_{\mu ,\mathbf{k}}^{(\text{opt})}\rangle$ labelled by μ = 1 … N:

This ensures “global smoothness of connection” and an optimal k-point connectivity by minimizing the gauge invariant term of the spread of the resulting WFs [43]. Afterwards, the spread-minimization is performed as usual using the Ψ^(opt). This allows to define the projector functions as:

It is important to note that while the projection of the KS Hamiltonian onto a given set of Wannier functions may reproduce the Kohn-Sham bands perfectly, different Wannierization choices may lead to different constructions of the orbitals and to different tight binding parameters. This issue is discussed in more detail in Ref. [44].

3.1.3 Comparison

The projector and Wannier constructions of the localized orbitals are conceptually very similar, differing in the specifics of how the correlated orbitals are constructed. The projector method is connected in a intuitively appealing manner to the local orbitals of interest (especially if the projection window $\mathcal{W}$ is set to a wide value), and provides a more convenient construction of double counting correction formulas [45]. In most applications to date the projector method is used only to construct the correlated orbitals needed in the DMFT procedure. Part of the motivation for this choice is to focus the DMFT treatment on the strongly correlated orbitals not well treated by DFT. The method avoids the expensive and sometimes unstable spread minimization associated with the Wannier construction.

The MLWF method is less dependent on an a-priori choice of atomic orbitals, is based on minimization of a clear metric under which the orbitals are constructed, and also minimizes deviations from the KS dispersion. Because it constructs a basis set which is complete within some energy range, it provides at no additional complication a full tight-binding parametrization of the electronic band structure in a given energy range,

providing physical intuition about the relevant orbitals. (With some effort, similar information can be obtained from the projector method, but this is not often done). Figure 3 shows two examples of fitting the NdNiO₂ low-energy KS states using MLWF. The first [Figure 3A], constructs 17 Wannier orbitals for all 17 KS states that are present in a large energy window from -9 to 8 eV, whereas the second [Figure 3B] constructs a minimal model only for the three frontier orbitals (Ni-$d_{x^2-y^2}$, Nd-$d_{z^2}$, Nd-d_xy). As shown in Ref. [21] an improved description of the low energy dispersion is obtained by the inclusion of a non-Ni, non-Nd, band orbital near the Fermi level, apparently representing interstitial charge, which is further discussed in Section 4.1.

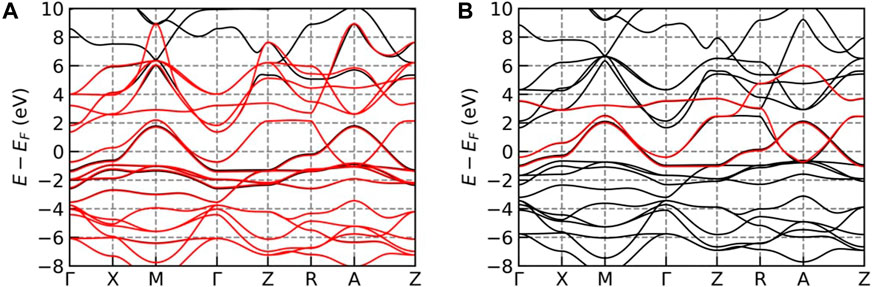
FIGURE 3. DFT bands for NdNiO₂ (black lines) and Winner fits (red lines) for Wannierization using (A) 17 Wannier functions (5 Nd-d orbitals +5 Ni-d orbitals + 6 oxygen-p orbitals + interstitial-s orbital and (B) using 3 Wannier functions (Nd-$d_{3z^2-r^2}$, Nd-d_xy and Ni-$d_{x^2-y^2}$ orbital). Adapted from Ref. [21].

In the following we will call all calculations performed directly in the tight-binding (TB) basis Wannier-mode calculations, whereas calculations in which the DMFT equations are written in the Kohn-Sham basis will be referred to as Bloch-mode calculations. Note, that direct formulation of the DMFT equations as a solution of a Hamiltonian restricted to the space of the correlated orbitals is in general not possible, because the projectors are in general non-square matrices and hence do not serve as a unitary transformation [46].

While Wannier and projector methods had until recently been viewed as roughly equivalent methods of constructing the basis in which the dynamical mean field equations are formulated, and indeed in some cases the equivalence of projector and Wannier-based methods was demonstrated [47], Karp et al. [44] found that results of the DFT + DMFT methodology can be sensitive to the choice of method used to construct the local orbitals of the downfolded model. We will review and discuss these results in Section 4.2.

3.2 Interactions in the Correlated Subspace

3.2.1 Basic Definitions

Once an orbital downfolding has been defined one has to formulate an appropriate interaction among the downfolded correlated orbitals $|{\varphi }_m^{R_i}\rangle$. Within the DMFT approximation the important interaction matrix elements are the on-site ones among the n correlated orbitals centered on the same site R_i. We begin by considering the matrix elements of the bare Coulomb interaction V among the correlated orbitals on a given site:

Here, $c_{m\sigma }^{†}$ and c_mσ are creation and annihilation operators for the correlated orbitals $|w_{\alpha }\rangle =|w_{,m,\sigma }^{R_i}\rangle$ or $|{\tilde{\varphi }}_m^{R_i}\rangle$, and $V_{m{m}^{\prime }{m}^{\prime \prime }{m}^{\prime \prime \prime }}$ is the Coulomb interaction tensor:

In the absence of symmetries there are $\mathcal{O}{n}^4$ matrix elements, but the main cases of physical interest involve a high degree of symmetry that enables one to reduce the complexity of the Coulomb tensor to just a few parameters. We will only describe the most important formulas here and refer the reader to Ref. [48] for an more detailed overview.

The most widely used form is the so called “Slater” parametrization [49], which makes use of the spherical symmetry of an isolated single atom. If the projectors in Eq. 3 are chosen to produce sufficiently local WFs this is a good approximation, and is for example used in all DFT + U implementations.

The most important Coulomb integrals are elements of $V_{m{m}^{\prime }{m}^{\prime \prime }{m}^{\prime \prime \prime }}$ that differ only in up to two different indices m. Using the symmetries this allows to define (in the absence of spin-orbit coupling):

Here, F^k, refers to the kth Slater integral, proportional in effect to the kth-pole of the electric charge distribution of the atomic configuration of the rotationally symmetric free-ion case. From the F^k the full Coulomb tensor can be constructed. For a d-shell of an isolated ion one can further show that

and that F⁴/F² is fixed, so that the entire Coulomb interaction tensor is determined by only two parameters: F⁰ = U_avg and J_avg. The ratio F⁴/F² is obtained empirically, varies only little for transition metals, and it is often fixed to F⁴/F² ≈ 0.625 [50].

Another often applied parametrization is the so called “Hubbard-Kanamori” form [51, 52], widely used in particular to describe the on-site interactions among electrons in the d-shell of a transition metal ion. This parametrization is formulated in terms of the averaged parameters:

which are the so-called Hubbard-Kanamori parameters for n orbitals. In the particular case of an octahedral crystal field, the d shell is split into a t_2g and e_g manifold. Within either the t_2g and e_g sub-manifold of the octahedral point group (but not for the whole d shell), one can verify that ${\mathcal{U}}^{\prime }=\mathcal{U}-2\mathcal{J}$ and $\mathcal{J}={\mathcal{J}}_C$ so as in the free ion case the full interaction can be constructed from only two independent parameters $\mathcal{U}$, and $\mathcal{J}$. The resulting interaction operator has the following form:

Importantly, this form of the interaction is rotationally invariant, which means that within the subset of orbitals, arbitrary unitary transformations on the orbitals can be applied, without adapting the parameters.

Note, that in this form $\mathcal{U}$ represents directly the diagonal terms of the full Coulomb tensor in contrast to the Slater parameter F⁰. In the case of spherical symmetry one can show that the two parametrizations are related by:

3.2.2 Determining the Screened Interactions

In solids the interaction parameters are renormalized from their bare values by screening processes V → U involving the other electrons in the solid. The most important renormalization is of the monopole interaction F₀ ≡ U_avg which gives the charging energy $E_C=\frac{1}{2}{U}_{avg}{N}_{tot}^2$ with N_tot = ∑_mn_m the total charge in the correlated orbitals. The charging energy measures the change in energy when the local charge is changed, but changing the local charge implies changing the ‘monopole’ electric fields produced by these charges; these electric fields are screened by the dielectric constant ϵ so that in computing the energy one should replace e²/r by e²/(ϵr) in Eq. 16 where ϵ is the dielectric constant associated with charge fluctuations on orbitals not included in the low energy theory. Since typical values of ϵ are ∼$5-10$ renormalizations of the charging energy from the free ion value ∼$20$ eV to solid state values of the order of 5 eV are expected. The other “J” terms represent energetics associated with electron rearrangement at fixed total charge, i.e., with changes in the quadrupole and octupole moments of the ion; these fields fall off much more rapidly and the J are as a result much more weakly screened, typically deviating by only 10–20% from the free-ion values. The important conclusion from this argument is that the basic interaction strength U or F⁰ depends on how the screening is treated. In the next sections we discuss this issue in more detail.

Commonly used ab-initio methods for treating the strong renormalizations from solid state screening are the constrained LDA method [53] and the constrained random phase approximation (cRPA) method [54]. Here, we present the latter, for a review see e.g., Ref. [55].

cRPA is a linear response theory based on the polarization function P giving the response of electrons to a test charge in the system. Within the RPA approximation, which neglects all non-Hartree terms, the dielectric function is calculated from the full bare Coulomb interaction and the polarization function as:

The polarization function P in RPA is calculated from DFT as:

where Ψ_νk and ϵ_νk mark KS eigenstates and eigenvalues.

The effective screened Coulomb interaction U in a target “(t)” space (typically the manifold of correlated states)can now be calculated as follows. Consider the example depicted in Figure 4. The effective screened Coulomb interaction is calculated by first splitting the polarization of the system in two parts, P_t pertaining only to transitions among the target orbitals and P_r containing all other transitions (including from target to non-target orbitals and the reverse):

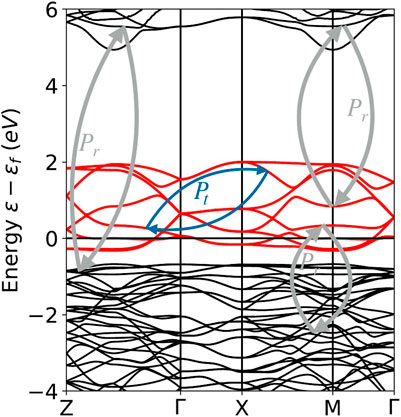
FIGURE 4. Band structure of LuNiO₃, with constructed Wannier functions for the Ni e_g states as target states t. The decomposition in the polarization channels P_t within the correlated subspace, and the polarization channels P_r outside, from, and to the target subspace t are schematically depicted as blue and grey arrows.

Now one can deduce the partially screened interaction W_r from P_r as:

Here W_r, which is implicitly restricted to include only matrix elements among the target orbitals, is Coulomb interaction tensor $U_{m{m}^{\prime }{m}^{\prime \prime }{m}^{\prime \prime \prime }}$ for the target orbitals, screened by transitions involving other orbitals. Because the screening involves only the non-target orbitals it is referred to as “constrained”. Adding the polarization P_t to P_r would recover the fully screened interaction

Note, that due to the energy dependency of the polarization, W_r is naturally frequency dependent. The frequency dependence is often neglected and U (ω = 0) is used.

Now, one can analyze the symmetries of the calculated Coulomb tensor and fit to one of the two forms given above. Either by directly averaging the elements of the tensor, or using a minimization procedure to minimize differences between U^cRPA and a constructed U. Importantly, U should be evaluated in the same orbitals used for the embedding techniques. We advocate the use of a more advanced version of cRPA for disentangled bands implemented in VASP evaluating the polarization directly using the WFs [56].

It is evident that the screening depends crucially on the chosen subspace. For example, a larger energy window for the target space in the downfolding produces more atomic like orbitals but also has fewer screening channels, so leads to a larger interaction, whereas smaller energy windows give more extended orbitals with smaller, heavily screened, interactions. As we will show later in Section 4.2 the screening in infinite layer nickelates is very sensitive as both, oxygen p states below, and Nd d states above, make large contributions to the screening. We discuss results from cRPA in Section 4.3.

3.3 Including Local Coulomb Interactions on Oxygen: DFT + sicDMFT Approach

In standard DFT + DMFT the many-body physics imposed by U on Ni is treated within the DMFT correlated subspace, however the description of the quantum processes on O remains on the Kohn-Sham DFT level. Note that correlations on the O (2p) orbitals are not necessarily weak because these orbitals, just as Ni(3d) ones, carry the first new angular-momentum number with growing main quantum number (there is neither a 1p nor a 2d orbital), meaning the orbitals may sit close to the atomic nucleus and therefore are more compact and with a larger charging energy. This implies that also 2p frontier orbitals have a demanding pseudopotential that needs to moderate between localization and itinerancy (though not as severely as for 3d orbitals). And this nature becomes increasingly relevant when the connection to the environment via a Δ comparable to U is substantial, a feature taking place for later TMOs. This suggests that a DFT-level treatment may be insufficient to tackle the sophisticated Mott-Hubbard vs. charge-transfer balance. As a further aspect in infinite-layer nickelates, while Ni-$d_{x^2-y^2}$ is strongly hybridized with O(2p), Ni-$d_{3z^2-r^2}$ is less so due to the missing apical oxygen. Hence the Ni-e_g {3z² − r², x² − y²} orbitals of the DMFT-active Ni(3d) shell are quite differently affected by O(2p). This may also call for an improved description of correlation effects originating from oxygen.

However, treating explicit Coulomb interaction within DMFT also for O(2p) raises several methodological and numerical challenges, and the explicit quantum-fluctuating aspect in these orbitals should be still generally weaker than in transition-metal 3d orbitals. In order to include localization tendencies on the oxygen sites beyond KS-DFT, one may therefore introduce the self-interaction correction (SIC) [34] as a simplified treatment compared to DMFT. The SIC scheme can efficiently be applied already on the pseudopotential level [57–59], leading to a refined O pseudopotential to be used in a standard CSC DFT + DMFT [60]. Use of this pseudopotential defines the DFT + sicDMFT method, which is thus capable of handling correlation physics on and between Ni and O closer to equal footing.

Figures 5A,B show the principal impact of the SIC inclusion on the DFT level. We see that the radial part of the O (2p) pseudopotential is somewhat reduced within the lower-limit of the bonding region (∼ 0.5–2 a.u.), resulting in a stronger localization of charge near the O site. For the NdNiO₂ crystal calculation within DFT + sic, i.e., employing the revised oxygen pseudopotential in the conventional KS cycle, two key effects may be observed. First, the O(2p) block of six bands (originally between $\sim [-3.5,-8]$ eV) get shifted to deeper energies, hence the p − d splitting is increased. Second, especially around the Fermi level, some band-narrowing takes place due to the renormalized hoppings resulting from the increased charge localization. It is important to note however that here these bands are an intermediate step in the full DFT + sicDMFT scheme, not a final physical result and are shown to provide insight into the physics underlying the method. In particular, the upward shift of the self-doping band away from the Fermi level is an artifact of the neglect of the local Coulomb interactions on Ni. The complete DFT + sicDMFT scheme yields the self-doping band again back at the Fermi level, which we will discuss in detail in Section 4.3.

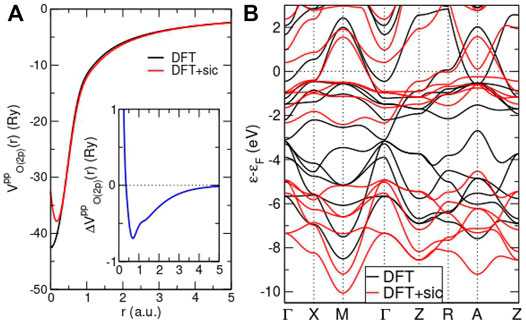
FIGURE 5. Effects of SIC inclusion on the DFT level. (A) Radial part of oxygen 2p pseudopotential with (red) and without SIC (black). Inset: difference between DFT and DFT + sic pseudopotential. (B) Band structure for NdNiO₂ within DFT (black) and DFT + sic (red). Note that in the latter calculation, SIC was only applied to O and the Ni orbitals are treated on the DFT level. F.L. to be published.

4 Results

In this section, we give an overview of results on infinite-layer nickelates in literature and a comparison to the better understood case of the layered copper oxides. We mainly focus on theoretical results [12, 13, 15–19, 21, 23, 27, 33, 44, 61–85] but present some comparison to experiments [4, 10, 86–98], when the relevant experimental results are available. We also mention that while we are aware of the important works on the study of interface effects [63, 65, 69], due to space limitation, we concentrate on the study of bulk nickelates here.

We present four levels of results: for orientation we show the DFT-level electronic structure; then we describe the basic many-body electronic structure following from the different DFT + DMFT calculations and the approximate physical picture that results. Next we consider the predictions of these calculations for the Fermiology–which bands are present at the Fermi surface and what are the mass enhancements. Finally, inspired by recent experimental results, we make some brief remarks about magnetism in Section 4.4.

4.1 DFT Results

Figure 6 compares basic aspects of the DFT-level electronic structure of the infinite layer nickelates NdNiO₂ and the analogous cuprate compound CaCuO₂. Panels a and d present the DFT bands of the two compounds. Panel d shows the familiar cuprate band structure, with one essentially two dimensional band of mixed Cu-$d_{x^2-y^2}$/O-2p_σ character crossing the Fermi surface. Panel a shows that in NdNiO₂ the situation is richer, with other Fermi surface crossings in addition to the Ni-$d_{x^2-y^2}$-derived band (highlighted in red) [21, 24, 26, 83, 99, 100]. The Fermi surfaces shown in panels b and e reveal that in addition to the $d_{x^2-y^2}$ bands which disperse very weakly in the z direction and give rise to a cylindrical Fermi surface sheet, there are two additional closed (three dimensional) electron pockets centered at Γ and A. The three dimensional sheets arise from Nd-d orbitals, in particular $d_{3z^2-r^2}$ and d_xy orbitals, with an admixture of Ni-$d_{3z^2-r^2}$ and d_xz/yz as well as interstitial states not directly attributed to any atomic orbital [21, 24, 25, 100, 101].

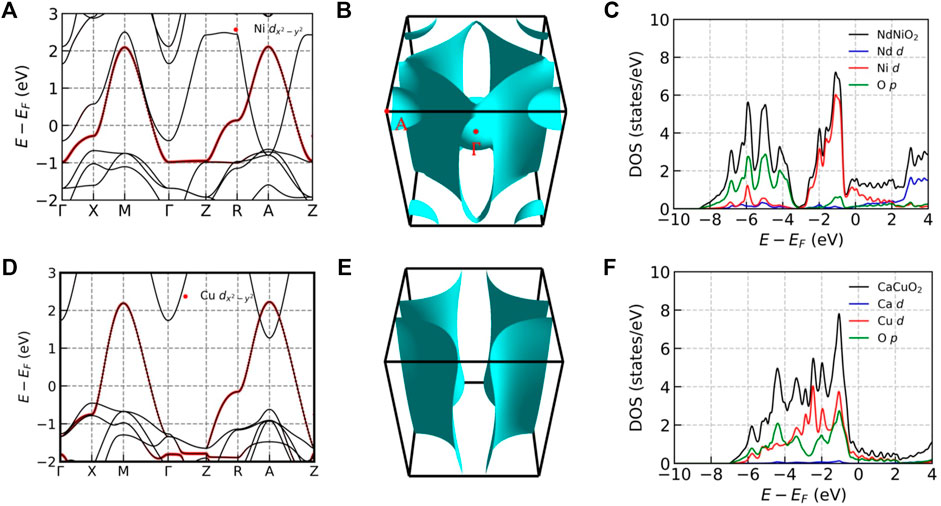
FIGURE 6. (A–C): Electronic properties of NdNiO₂. (A): Electronic band structure of NdNiO₂ close to the Fermi level. The red dots highlight the Ni $d_{x^2-y^2}$ band. A second band also crosses the Fermi level. (B): Fermi surface of NdNiO₂. In addition to the cylindrical Fermi sheet that is derived from Ni $d_{x^2-y^2}$ band, there are two additional electron pockets: one is at Γ = (0, 0, 0) and the other is at A = (π, π, π). (C): Densities of states of NdNiO₂. The black, blue, red and green curves correspond to total, Nd-d projected, Ni-d projected and O-p projected densities of states, respectively. The Fermi level is shifted to the zero point. (D–F): Electronic properties of CaCuO₂. (D): Electronic band structure of CaCuO₂ close to the Fermi level. The red dots highlight the Cu $d_{x^2-y^2}$ band. (E): Fermi surface of CaCuO₂. (F): Densities of states of CaCuO₂. The black, blue, red, and green curves correspond to total, Ca-d projected, Cu-d projected, and O-p projected densities of states, respectively. The Fermi level is shifted to the zero point. Adapted from Ref. [21].

Charge transfer from the $d_{x^2-y^2}$-derived band to the Nd-derived band leads to a “self-doping” effect: in the stoichiometric infinite layer nickelate compound the $d_{x^2-y^2}$-derived band is not half-filled; rather its occupancy corresponds to about a 10–15% hole doping filling; thus stoichiometric nickelates should be compared to hole-doped cuprates.

It is important to note that the published DFT analyses of orbital admixture are obtained by projecting the states onto atomic orbitals as described in the projector section above. Gu et al. [21] find via a Wannier analysis that the additional band also has considerable contribution from charge density not centered on any atom. Because this component is not centered on an atom it is not easily revealed in the standard projector analysis. Panel a of Figure 7 shows this component, known as an interstitial s orbital, which is located at the mid-point between two neighboring Ni atoms along the z axis. Panels b and c show the fitting of DFT band structure using maximally localized Wannier functions (MLWF) as explained in the previous Methods section. Panel b shows a band fit based on 16 MLWFs, of which 5 are initialized as being centered on Ni-d orbitals, five more centered on Nd-d orbitals and six O-p orbitals. The fitting is very good for the occupied bands but for one of the Nd-derived empty bands, the Z → R portion is not well reproduced. Panel c shows the result of adding one more MLWF that corresponds to the interstitial s orbital. The fitting is improved, in particular in that Nd-derived bands are now exactly reproduced throughout the first Brillouin zone. Panel d shows the weight of the interstitial s orbital on the different bands. We can see that the s-orbital has a high weight on the extra band on the Z → R portion at energy E ≈ 2 eV above the Fermi level.

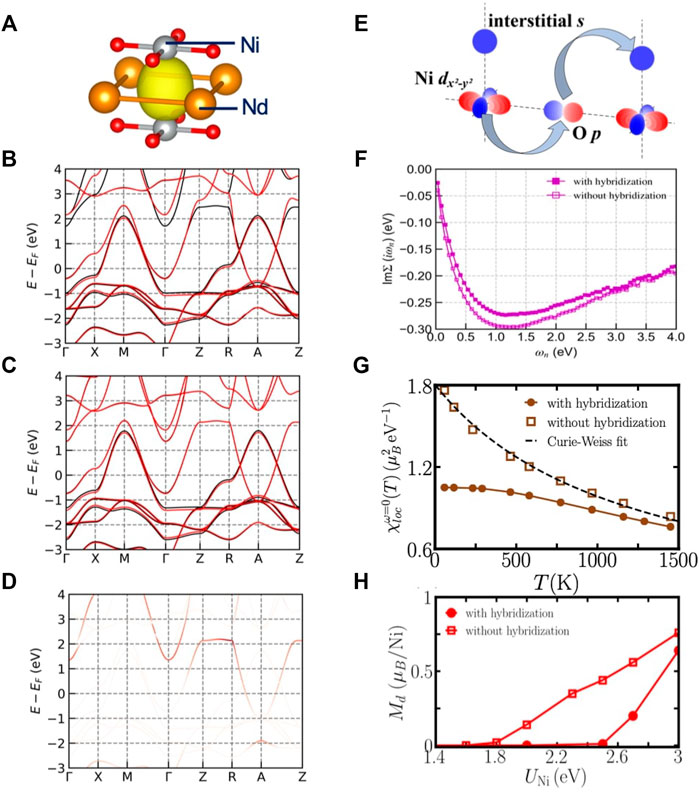
FIGURE 7. (A): An iso-value surface of the interstitial s orbital in NdNiO₂. (B): Fitting of DFT band structure of NdNiO₂, using 16 Wannier functions (Nd-d, Ni-d, and O-p orbitals). The black lines are DFT bands and the red lines are fitted bands from Wannier functions. (C): Fitting of DFT band structure of NdNiO₂, using 17 Wannier functions (Nd-d, Ni-d, O-p, and the interstitial s orbitals). The black and red lines have the same meaning as in panel (B). (D): The fatband plot of the interstitial s orbital. (E): An illustration of the hybridization between Ni $d_{x^2-y^2}$ orbital and the interstitital s orbital via a second-nearest-neighbor hopping. (F): Imaginary part of the self-energy of Ni $d_{x^2-y^2}$ orbital calculated using DFT + DMFT method with hybridization (solid symbols) and without hybridization (open symbols). (G): Local susceptibility ${\chi }_{\text{loc}}^{\omega =0}(T)$ of NdNiO₂ as a function of temperature calculated with hybridization (solid symbols) and without hybridization (open symbols). The dashed line is a Curie-Weiss fitting. (H): Magnetic moment on Ni d orbitals as a function of interaction strength ${\mathcal{U}}_{\text{Ni}}$ calculated with hybridization (solid symbols) and without hybridization (open symbols). Adapted from Ref. [21].

One of the key questions in the materials physics of the layered d⁹ nickelates is whether the additional band is a “spectator”, acting simply as a reservoir enabling charge transfer from the NiO₂ plane to the Nd spacer layer, or whether the additional band also plays an essential role in the physics, either because it is strongly hybridized with or strongly interacting with the Ni degrees of freedom. The orbital composition of the additional band is relevant to this question: the “spectator band” contains Nd $d_{3z^2-r^2}$ and d_xy orbitals, as well as a small but non-zero admixture of Ni $d_{3z^2-r^2}$ and d_xz/yz content; however the hybridization of these orbitals to the Ni $d_{x^2-y^2}$ band is very weak. However, in the Wannierization with the interstitial charge included, the hybridization between the interstitial s orbital and Ni $d_{x^2-y^2}$ is one order of magnitude stronger [21]. Panel e of Figure 7 shows the hybridization between Ni $d_{x^2-y^2}$ and the interstitial s orbital via the second-nearest-neighbor hopping. Because of this hopping, the itinerant electrons in the Nd spacer layer can effectively interact with the electrons in Ni $d_{x^2-y^2}$ orbital and therefore it is suggested that this coupling may lead to Kondo-type physics [102, 103].

To complete the discussion of DFT-level theory we mention DFT + U calculations on infinite-layer nickelates. In these calculations all the atomic orbitals that are in the pseudo-potentials are taken into account [11, 24, 26] and rotationally invariant Hubbard U interactions are added on all the five Ni d orbitals. Botana et al. [24] extracted various hopping matrices and energy splitting, which shows similarity between infinite-layer nickelates and cuprates. Kapeghian et al. [26], Been et al. [11] and Xia et al. [104] studied the electronic structure trends of the entire lanthanide series of infinite-layer nickelates.

4.2 DFT + DMFT: Local Electronic Structure

In transition metal oxides, it is believed that the interesting correlation physics arises from a competition between local interactions within the transition metal d-shell, which control the relative energetics of different d-multiplets, and the hybridization with other orbitals, which acts to mix the d-multiplets. In assessing the relevance of different interactions, an analysis of the ground state wave function is of interest. As noted previously, a formal valence analysis places either the Ni or the Cu in a d⁹ state, thus with one hole in the d-shell and full oxygen-2p and empty Nd-5d/6s shells. Deviations from this simple picture provide insight into the relevant interaction processes. One question is the admixture of ligand (O-2p holes in the cuprate and nickelate cases and also Nd-5d/6s electrons in the nickelate case) states. One distinguishes [105] “charge transfer” materials where the energy difference between the ligand and transition metal d states controls the physics from Mott Hubbard materials where the charging energy of the transition metal d-shells controls the physics. A second issue is the relative weight of different transition metal multiplets. In “Hund’s metals”, multiplet configurations involving high spin (spin S ≥ 1) d-states are relevant; in Mott Hubbard materials only the S = 1/2 and S = 0 states are relevant.

DFT + DMFT calculations provide theoretical estimates of orbital occupancies and of the local density matrices describing the multiplet probabilities of the correlated sites and the occupancies of the ligand sites. In the cuprate case there is general agreement both within DFT and in DFT + DMFT that the only relevant states are d⁹ (with the hole in the Cu-$d_{x^2-y^2}$ orbital) and $d^{10}\underline{L}$. These two states appear with almost equal weight, while the Cu d⁸ configuration plays a negligible role (for a recent calculation consistent with the substantial previous literature see [33]). This pattern of occupancies marks the cuprate material as a “charge transfer” compound [105] in which the major deviation from the atomic limit comes from moving the d-shell hole onto the oxygen network and back and the correlation physics should be thought of as arising from the oxygen-copper hybridization in the presence of strong local Cu correlations.

In the nickelate compounds the theoretical situation is less clear. There is a general consensus that the Ni-$d_{x^2-y^2}$ orbital is occupied by approximately one electron, and that the oxygen states are farther removed in energy from the $d_{x^2-y^2}$ orbital than in the cuprates and also more weakly hybridized, implying the admixture of the oxygen states into the near Fermi level bands is smaller than in cuprates [23, 24, 27, 75, 106]. There is also general consensus that charge transfer onto the Nd states occurs. However, whether NdNiO₂ is in the Mott-Hubbard region or in a critical region with mixed charge-transfer/Mott-Hubbard character is still under debate [23, 75, 107]. Another complication arises from the interstitial s orbital, which hybridizes with the Ni-$d_{x^2-y^2}$ orbital. Panels f, g and h of Figure 7 compare the imaginary part of the self-energy of Ni-$d_{x^2-y^2}$ orbital, the local susceptibility and magnetic phase diagram of NdNiO₂ with the hybridization (solid symbols) and without the hybridization (open symbols) [21], calculated using DFT + DMFT method (U_Ni = 2 eV) that is explained in the Methods section. Panel f shows ImΣ(iω_n) of Ni-$d_{x^2-y^2}$ orbital. The effective mass $\frac{m^{\ast }}{m}\simeq 1-\frac{d\mathrm{I}\mathrm{m}(i{\omega }_n)}{d{\omega }_n}{|}_{{\omega }_n\to 0}$ is reduced from 2.0 without hybridization to 1.8 with hybridization. Panel g shows the local susceptibility ${\chi }_{\text{loc}}^{\omega =0}(T)={\int }_0^{\beta }{\chi }_{\text{loc}}(\tau )d\tau ={\int }_0^{\beta }{g}^2⟨S_z(\tau )S_z(0)⟩d\tau$. The hybridization reduces ${\chi }_{\text{loc}}^{\omega =0}(T)$ at low temperatures, indicating the screening of the Ni spin in $d_{x^2-y^2}$ orbital. Panel h shows the magnetic moment on Ni atom as a function of interaction strength $\mathcal{U}$ on Ni-$d_{x^2-y^2}$ orbital. The hybridization increases the critical $\mathcal{U}$ that is needed to stabilize long-range antiferromagnetic ordering. Overall, the presence of the hybridization makes Ni-$d_{x^2-y^2}$ orbital less correlated and less magnetic, which is consistent with the Kondo screening picture.

Perhaps more importantly, unlike the cuprate case the transition metal Ni-$d_{3z^2-r^2}$ may also be relevant. The Ni-$d_{3z^2-r^2}$ has a non-negligible hybridization with the Nd-$d_{3z^2-r^2}$ band, so the three dimensional bands may be more than spectator bands, and instead participate to some degree in the correlation physics and Hund’s physics may be relevant. Karp et al. [25, 27] find $\le 15\%$ high spin d⁸ and argue that only the Ni-$d_{x^2-y^2}$ orbital is important for the low-energy physics. Wang et al. [16] find 25.9% high spin d⁸ (10.8% low spin d⁸) in the ground state configuration of LaNiO₂ and argue based on this that the material should be classified as a Hund’s metal. A difference between the calculations is the number of correlated d orbitals retained. The result of Wang et al. [16] is in partial agreement with the GW + EDMFT study of Petocchi et al. [79] which also finds $\sim 25\%$ high spin d⁸ character ($\sim 25\%$ low spin d⁸) at optimal doping level. However, Petocchi et al. [79] report a nonmonotonic doping dependence of the high-spin d⁸ weight, whereas Ref. [16] reports a monotonic doping dependence. Petocchi et al. [79] point out that the effect of this physics on the low energy properties is not clear.

These questions are not theoretically settled because, as shown by Karp et al. [44] the choice of method used to construct the local orbitals of the downfolded model affects the DMFT results for the nickelate. Table 1 compares the orbital occupancies and multiplet occurence probabilities (defined as weight of the different configurations in the many-body density matrix projected onto the Ni states) obtained with different methodologies.

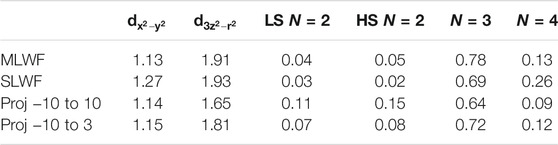
TABLE 1. Orbital occupancies of the most relevant Ni-d orbitals of NdNiO₂ from the Matsubara Green function (left) and occurrence probabilities of low spin (LS S = 0) and high spin (HS S = 1) multiplet configurations obtained from the impurity density matrix computed for stoichiometric NdNiO₂ using a Kanamori Hamiltonian with two correlated orbitals and $\mathcal{U}=7$ eV and $\mathcal{J}=0.7$ eV at T = 290K. From Ref. [44].

4.3 DMFT Theory of the Low Energy Physics

We next consider the consequences of the wide window electronic structure for the low energy physics. Panels (a) and (b) of Figure 8 show the many body electronic structure (momentum and frequency dependent electron spectral function) computed for NdNiO₂ at two representative dopings using the basic DFT + DMFT and DFT + sicDMFT methods for a particular method and choice of parameters. From a comparison with other nickelates [60] and in view of experimental constraints (see discussion in [106]) a value U_avg = 10 eV and J_avg = 1 eV is here used to parametrize the local Coulomb interaction for the Ni(3d) orbitals in charge self-consistent DFT+(sic)DMFT calculations. The projector method for the five Ni(3d) orbitals, building on the 12 KS states above the O(2s) bands [i.e., an energy window (−10, 3) eV], is employed and a rotational-invariant Slater Hamiltonian is active in the resulting correlated subspace. The hole doping δ is achieved by the virtual-crystal approximation using an effective Nd atom [108], where the Nd (4f) states are frozen in the pseudopotential core. Note again that calculational settings resulting in the data shown in Figure 8 differ only in using the LDA (SIC) oxygen pseudpotential in DFT+(sic)DMFT.

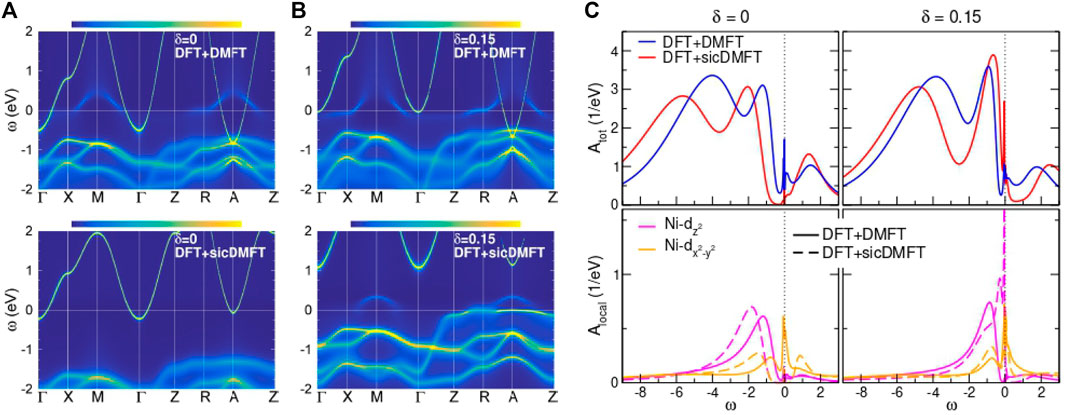
FIGURE 8. Comparison between DFT + DMFT and DFT + sicDMFT at T = 30 K, using U_avg = 10 eV, J_avg = 1 eV and projected-local orbitals on the 12 KS states above the O(2s) bands for both schemes, respectively. (A,B) k-resolved spectral function A (k, ω) for (A) pristine and (B) δ = 0.15 hole-doped NdNiO₂. (C) Total and Ni-e_g local spectral function for both doping cases. Adapted from [108].

The upper panels of Figures 8A,B show the DFT + DMFT spectral function. In comparison to the DFT bands shown in Fig. 6, we see that the Ni-$d_{x^2-y^2}$-derived band is narrowed and broadened, and its separation in energy from the lower lying Ni-t_2g and O(2p) bands is increased. The lower panels show the DFT + sicDMFT results, which are markedly different. We see that in the stoichiometric compound the $d_{x^2-y^2}$ bands are completely absent: within this scheme these orbitals are completely localized and incoherent, hence not visible in the spectral function. The position of the “spectator” bands relative to the Fermi surface is also changed, with some electrons transferred to these orbitals [20]. This may calls for an alternative possible Kondo scenario at low T, including also a substantial role of the Ni-$d_{3z^2-r^2}$ orbital [20]. At doping δ = 0.15 we see that in the DFT + sicDMFT calculation some aspects of the $d_{x^2-y^2}$ bands are restored, but again the relative positions of the spectator and $d_{x^2-y^2}$ bands are very different in the two methods. Panel (c) of Figure 8 shows the momentum integrated total and Ni-projected spectral functions. Important differences between the results of the two methods include the p − d splitting visible as the shift in higher binding energy peak from ∼$-4$ eV to ∼$-6$ eV (cf upper left panel) and the proximity of the $d_{3z^2-r^2}$ states to the Fermi surface. This characterizes the material as an effective orbital-selective Mott-insulator. In this theory, hole doping leaves the Ni-$d_{x^2-y^2}$ occupancy almost unchanged at half filling. Instead, the Ni-$d_{3z^2-r^2}$ orbital takes care of most of the charge doping and becomes significantly further depleted. Therefore within DFT + sicDMFT, the superconducting region is designated by the coexistence of nearly half-filled Ni-$d_{x^2-y^2}$ and a Ni-$d_{3z^2-r^2}$-based flat band crossing the Fermi level. As discussed in Ref. [108], this flat band interacts with the Mott-like state such as to increase coherency within the Ni-$d_{x^2-y^2}$ sector. For even larger hole doping, the system evolves into a bad Hund metal, where coherence is lost again [108]. Let us note that the shift of the Ni-$d_{3z^2-r^2}$-based flat band towards the Fermi level is supported by a full GW + EDMFT investigation [79].

As depicted in Figure 9, the increase of correlation strength with SIC inclusion originates from the stronger localization of O(2p) electrons. The oxygen states are shifted down in energy, leading to an increase of the p-d splitting and thus to a value Δ = 5 eV for the charge-transfer energy [106]. Figure 9B shows directly in real space, that the SIC-modified pseudopotential of oxygen enhances the 2p charge density around the oxygen sites, with additionally further depleting Ni-$d_{x^2-y^2}$. Hence in DFT + sicDMFT an adjustment of the U vs. Δ competition takes place, which refines furthermore the various hopping integrals of the system.

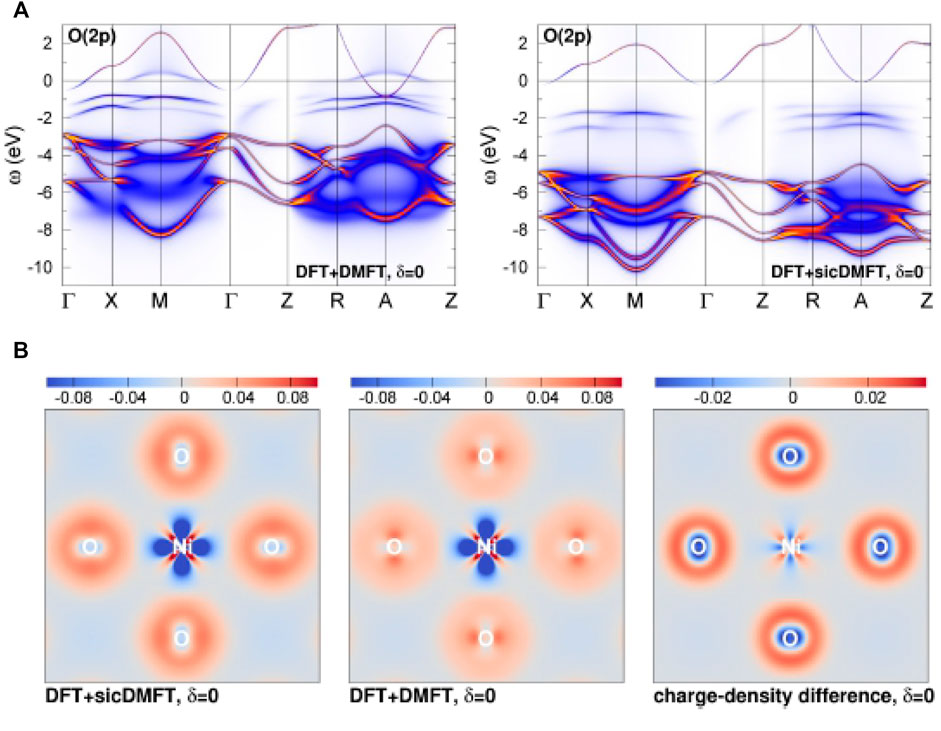
FIGURE 9. Oxygen 2p states in DFT + DMFT and DFT + sicDMFT. (A) Orbital weight (i.e., fatbands) in the interacting regime along high symmetry lines. (B) Interacting bond charge density $\rho -{\rho }_{\text{atom}}^{\text{LDA}}$, with right panel displaying the difference between the densities shown in the left and middle panel. F.L. to be published.

These results highlight the basic electronic structure questions: 1) what is the coherence (scattering rate and mass enhancement) of the Ni-$d_{x^2-y^2}$-derived band and 2) how strong are the interactions on the “spectator” bands? 3) what is the energy difference between the O-2p and $d_{x^2-y^2}$ orbitals. The different implementations of the DFT + DMFT methodology give different answers to these questions. 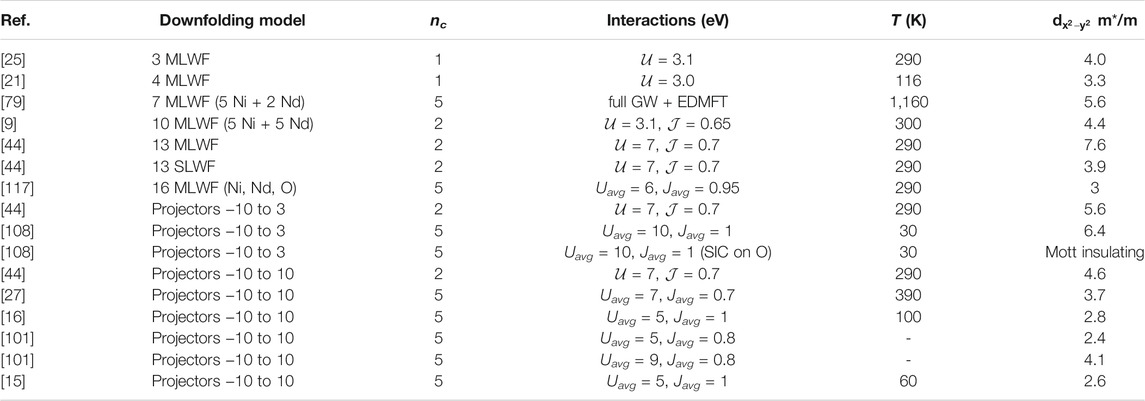While most methods, with the exception of the sic method, give a somewhat coherent $d_{x^2-y^2}$ band the estimates of the orbital mass enhancement vary substantially, as shown in Table 2. These quantities are experimentally accessible via photoemission experiments, and future experiment/theory comparisons will provide valuable methodological guidance. It should be noted that most papers only discuss orbital mass enhancements, which are generally larger than band enhancements, especially for large energy window calculations.

TABLE 2. $d_{x^2-y^2}$ orbital mass enhancement from different DMFT results in the literature. n_c refers to the number of correlated orbitals in the impurity problem.

The question of band renormalization in different downfolding choices is tightly coupled with the question of screening (see Section 3.2.2). cRPA studies showed that if a seven orbital downfolding model is constructed from five Ni(3d) orbitals and two Nd(5d) orbitals in a small energy window (not containing any oxygen states), the static part of the onsite Coulomb interaction is $U_{d_{x^2-y^2}}\approx 5$ eV [19, 79]. For a minimal model containing only the Ni $d_{x^2-y^2}$, the Nd $d_{3z^2-r^2}$, and the interstitial s orbital, $U_{d_{x^2-y^2}}$ is even further reduced to $\approx 3.1$ eV [19]. The bare Coulomb interaction is of the order of $V_{d_{x^2-y^2}}\approx 25$ eV, highlighting the strong screening of the low-energy states. The resulting strong frequency dependency, which is usually neglected in DFT + DMFT calculations, plays a crucial role leading to a mass enhancement in GW + EDMFT calculations comparable to that of DFT + DMFT calculations with much larger static $\mathcal{U}$ values (see Table 2) [79]. This shows, that the other orbitals close to the Fermi level play an important role in screening processes for the Ni $d_{x^2-y^2}$ correlations, and using static Coulomb interaction parameters from cRPA will lead to a underestimation of correlation effects in a small energy window downfolding scheme. This also raises the importance of inter-site interaction Coulomb matrix elements in a large energy window calculation between the Ni(3d) orbitals and O(2p) and Nd(5d) states.

Finally, we may consider the functional form of the self energy, which is relevant to the issue of Hund’s physics. Hund’s metal physics is believed to imply a particle-hole asymmetric structure in the self energy leading to an extra peak in the electron spectral function [33, 109]; for materials such as NdNiO₂ where the d-shell is more than half filled the peak is on the unoccupied part of the spectrum [33]. Conversely, Mott physics would result in a two peak spectral function and a more symmetric self energy with peaks on both sides. As shown in Figure 10, the $d_{x^2-y^2}$ self energy computed in [27] has strong (but broadened, especially on the positive frequency side) peaks at ω ≈ − 0.7eV and ω ≈ 2eV and the corresponding spectral function shows two Hubbard peaks and a central quasiparticle feature. These are consistent with expectations of a Mott-Hubbard material. In addition, a weak feature is visible as a change of concavity around ω = 0.2eV; comparison to spectra presented for the Hund’s metals Sr₂RuO₄ and Sr₂MoO₄ suggests that this may be a signature of weak Hund’s physics [33]. Wang et al. report a much larger d⁸ weight in the ground state but exhibit a similar $d_{x^2-y^2}$ spectral function, suggesting that the presence of some admixture of high-spin d⁸ does not strongly affect the low energy physics. Kang et al. [110] present a spectral function that shows a stronger feature (a peak) at about ω = 0.2eV on the unoccupied side of the spectral function at low temperatures, which may be a sign of Hund’s correlations. They also report a slope inversion on the occupied side which is not expected in the theory of Hund’s metals with more than half filled d-shells [33].

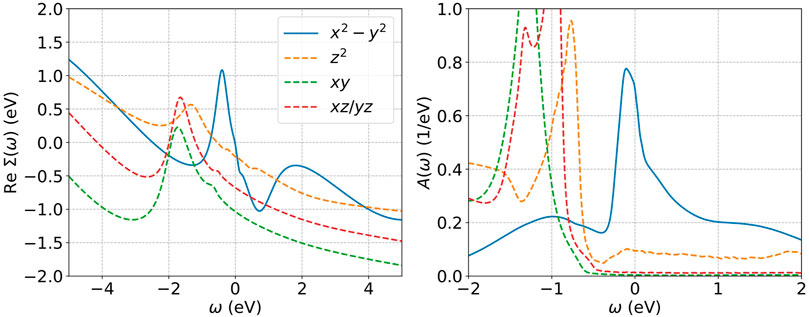
FIGURE 10. Left: Self energy of the different orbitals in a five orbital fully charge self consistent DFT + DMFT calculation at stoichiometry with projectors in an energy range from −10 to 10 eV around the Fermi level, using a rotationally invariant slater Hamiltonian with U_avg = 7 eV, J_avg = 0.7 eV, and T = 290K. Right: corresponding momentum integrated spectral function. Adapted from Ref. [27].

4.4 Magnetism

We now discuss briefly the magnetic properties. The stoichiometric cuprates are antiferromagnetic insulators, with a charge gap of approximately 1.5  eV, a Neel temperature $\approx 300$ K set by weak interlayer and spin orbit effects, and an intrinsically large magnetic scale evident for example as a zone boundary magnon energy $\approx 0.3$ eV. Fitting to a Heisenberg model implies a nearest neighbor exchange coupling J_NN ≈ 120 meV although it must be born in mind that the materials are intermediate coupling, so the magnetism is in a intermediate regime between itinerant and localized. Upon doping the commensurate magnetism vanishes rapidly but evidence of strong magnetic correlations (and in some materials tendency to incommensurate magnetic order) persists to a doping of about 0.15.

A discussion of magnetism in the nickelates is complicated by the self-doping effect. If the physics of the nickelates is directly comparable to that of the cuprates then one would expect the stoichiometric nickelates to be on the boundary of magnetism. Recent resonant inelastic X-ray (RIXS) [92] and nuclear magnetic resonance experiments [91] are consistent with this picture. In particular, Lu et al. report no long ranged order but observe a strong zone boundary paramagnon-like excitation implying a J_NN ≈ 60 meV, about half of the cuprate value.

Theoretically a number of DFT + U, hybrid DFT and DFT + DMFT studies have studied magnetism of infinite layer nickelates [17, 21, 24, 25, 84, 99, 101, 108, 111] and reported a wide range of magnetic superexchange [17, 18, 23, 66, 76, 77, 99, 112] from a small value of about 10 meV [23, 99] to an intermediate value of about 30 meV [66] to a large value of about 80–100 meV [17, 18, 76, 77, 112]. DFT + DMFT studies have not examined the Ni exchange coupling systematically. Further investigation of the magnetic properties within this method is likely to provide valuable insights.

5 Summary

DFT and beyond DFT analyses have produced a broadly coherent picture of the electronic structure of the infinite layer d⁹ nickelates. Similar to the cuprates there is a rather two dimensional Ni-$d_{x^2-y^2}$-derived band that is moderately to strongly correlated. Differently from the cuprates, at the Fermi surface there is an additional, much more three dimensional, band derived from the rare earth d-orbitals (with some admixture of interstitial charge and of Ni(3d) states). The energy difference between Ni(3d) and O(2p) orbitals is larger in the nickelates than the cuprates, putting the nickelates farther from the charge transfer regime than are the cuprates. Finally, in contrast to the cuprate materials where the only relevant configurations of the transition metal ions are the d⁹ and d¹⁰ states, in the nickelate materials some admixture of the high-spin d⁸ configuration occurs, raising the possibility of Hund’s metal physics.

Given this broad consensus, the question becomes which of the differences and similarities to the cuprates are important for the low energy physics. It is clear that the additional band “self-dopes” the Ni $d_{x^2-y^2}$ bands, so that the chemistry-doping phase diagram of the infinite layer nickelates is shifted from that of the cuprates by about 0.1 hole/Ni, and that charge transfer to the oxygen orbitals is less relevant in the nickelates than in the cuprates. The important open question is whether the other differences are important for the low energy correlation physics, in other words, whether the low energy physics of the infinite layer nickelates may be understood in terms of a one band Hubbard model or whether richer physics is needed. Answering this question bears directly on the issue of the mechanism for the observed superconductivity. This question is not yet settled, in part because different flavors of the DFT + DMFT have provided different quantitative answers to questions including the fractional weight of high spin d⁸ configurations in the ground state, the relative energy positions of the p and d band manifolds and what is the mass enhancement of the different bands near Fermi surface. Some of these differences may be traced to different choices required in the DFT + DMFT approach to correlated materials.

In this article we have explained the different choices and the different results that emerge. Some of the differences in results are experimentally testable. For example, the DFT + (sic)DMFT approach yield significantly more strongly correlated/less coherent $d_{x^2-y^2}$ derived bands and indeed different DFT + DMFT methods produce different mass enhancements. Thus angle-resolved photoemission measurements of the quasiparticle dispersion and linewidth, in combination with higher energy measurements of the p-d energy splitting, can experimentally test the different predictions. Hund’s metal physics is an intrinsically multiband effect, which involves characteristic asymmetries in the electron self energy. Even more importantly the known examples of Hund’s metals involve multiple strongly correlated bands crossing the Fermi surface. Detailed analyses of the structure of the electron dispersion and the strength of the correlations on the “spectator” bands will provide insight. There are also interesting differences in the theoretical predictions for magnetic properties and superconducting pairing [9, 14, 18, 64, 88, 113, 114], which future experiments may test. Finally, we note that our discussion is based on the single-site version of dynamical mean field theory. While model-system studies have shown that this approximation captures the main features of the wide energy range many-body electronic structure, the single-site approximation does not capture important aspects of the low energy physics, such as superconductivity or pseudogap physics. “Cluster” and related extensions (e.g., DΓA) of the theory are an important directions for future research [9].

We hope that our work will motivate comparisons to experiment and to more fundamental theoretical approaches that will help resolve some of the methodological questions relating to the DFT + DMFT approach to correlated materials.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

HC is supported by the National Natural Science Foundation of China under project number 11 774 236, the Ministry of Science and Technology of China under project number SQ2020YFE010418, and NYU University Research Challenge Fund. FL and JK were supported by grants from the Simons Foundation. The Flatiron Institute is a division of the Simons Foundation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

HC acknowledges useful discussions with Yuhao Gu, Mi Jiang, Danfeng Li, Jiawei Mei, Xiangang Wan, Tao Wu, Xianxin Wu, Yifeng Yang, Guangming Zhang, Zhicheng Zhong, Wei Zhu, and in particular, Chengliang Xia for his help in making part of the figures.

References